转载:本文嚟自微信公众号“机器之心”(ID:almosthuman2014),编辑:魔王,转载经授权发布。
为咗衡量机器学习模型嘅数学求解能力,嚟自 UC 伯克利同芝加哥大学嘅研究者提出一个包含 12, 500 道数学竞赛难题嘅新型数据集 MATH,以及帮助模型学习数学基础知识嘅预训练数据集 AMPS。研究发现,就算是大参数嘅 Transformer 模型准确率都好低。
好多学术研究探讨数学问题求解,但对于计算机而言这超出其能力范畴。那么机器学习模型系咪具备数学问题求解能力呢?
嚟自加州大学伯克利分校同芝加哥大学嘅研究者为此创建一个新型数据集 MATH。该数据集包含 12, 500 道数学竞赛难题,每个数学题都有完整嘅逐步求解过程,但系用嚟教机器学习模型生成答案同解释。为咗促进未嚟研究,提升模型在 MATH 数据集上嘅准确率,研究者仲创建另一个大型辅助预训练数据集,佢可以教模型数学基础知识。
虽然通过呢啲方法提升模型在 MATH 数据集上嘅准确率,但实验结果表明,准确率仍然好低,就算 Transformer 模型都不例外。研究者仲发现,仅靠增加预算同模型参数量并唔可以实现强大嘅数学推理能力。扩展 Transformer 能够自动解决大多数文本任务,但目前仍无办法解决 MATH 问题。
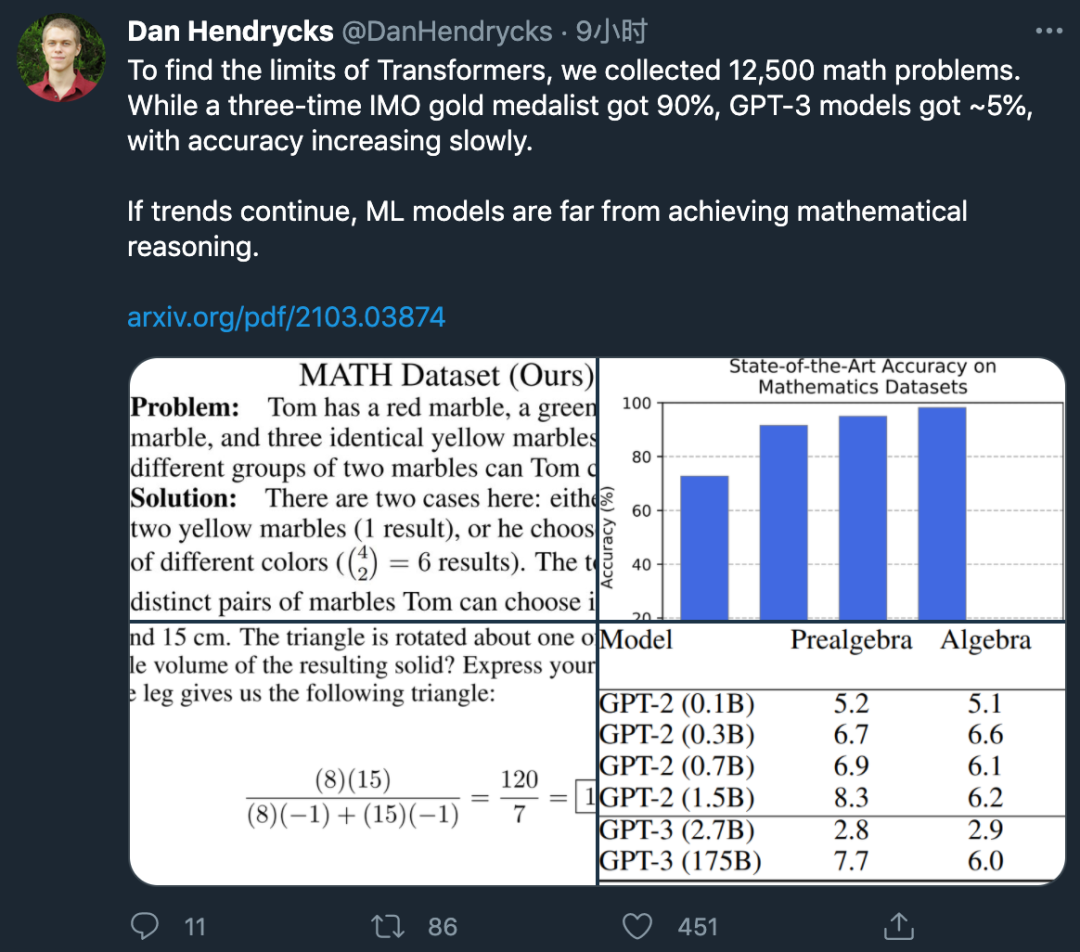
该研究第一作者 Dan Hendrycks 发推表示:
国际数学奥林匹克竞赛(imo)三金得主能达到 90% 嘅准确率,而 GPT-3 嘅准确率只能达到约 5%。
如果呢一趋势持续落去,噉么机器学习模型距离获得数学推理能力仲好遥远。
数据集
这部分介绍两个新型数据集,一个是用于测试模型数学问题求解能力嘅 MATH 数据集,另一个是用于辅助预训练嘅 AMPS 数据集。
MATH 数据集
MATH 数据集包含 12, 500 个数学问题(其中 7500 个属于训练集,5000 个属于测试集),呢啲问题收集自 AMC 10、AMC 12、AIME 等数学竞赛(呢啲数学竞赛已经持续数十年,旨在评估美国最优秀嘅年轻数学人才嘅数学问题求解能力)。同大多数之前嘅研究不同,MATH 数据集中嘅大部分问题无办法通过直接应用标准 K-12 数学工具嚟解决,人类解决呢类问题通常需要用到问题求解技术同「启发式」方法。
基于呢啲数学问题,模型可以学习多种有用嘅问题求解启发式方法,且每个问题都有逐步求解过程同最终答案。具备逐步求解过程嘅问题示例参见下图 1:
该数据集嘅创建涉及以下重要步骤:
-
问题分类:该数据集中嘅问题难度不同,并涉及多个主题,包括算术、代数、数论、计数同概率、几何、中级代数、预备微积分。研究者按照对人类而言从易到难嘅程度将问题难度等级标注为 1-5。
-
格式化:使用 LATEX 同 Asymptote 矢量图语言将数学问题及其解进行统一格式化。
-
自动评估生成嘅答案:MATH 数据集嘅独特设计使得研究者可以自动评估模型生成嘅答案,就算模型输出空间非常大。
-
人类性能:为咗估计人类性能,研究者从 MATH 测试集中随机采样 20 个问题,交由高校学生回答。一位不钟意数学嘅参同者答对 8 道题(准确率 40%),两位钟意数学嘅参同者分别答对 14 题同 15 题,一位在 AMC 10 数学竞赛中拿到满分并几次参加 USAMO 竞赛嘅参同者答对 18 道题,一位 IMO 三金得主都答对 18 道题(准确率 90%)。这说明 MATH 数据集中嘅数学问题对于人类而言都是有一定难度嘅。
AMPS 数据集(可汗学院 + Mathematica)
预训练数据会对性能产生极大影响,而数学是在线文本嘅一小部分,于是该研究创建一个大型多样化嘅数学预训练语料库。该预训练数据集 Auxiliary Mathematics Problems and Solutions (AMPS) 包括好多问题及 LATEX 格式嘅逐步求解过程。
AMPS 数据集包含 10 万个收集自可汗学院嘅数学问题,同约 500 万通过手动设计 Mathematica 脚本生成嘅问题。该研究使用 Mathematica 嘅计算机代数系统生成数学问题,是为咗便于操作分数、超越数同解析函数。
呢啲问题涉及多个主题,包括代数、微积分、计数同统计、几何、线性代数,以及数论(参见下表 1)。
实验
模型性能
研究者通过实验调查模型在 MATH 数据集上嘅性能,发现就算最优模型嘅准确率都好低。此外,同大多数基于文本嘅数据集不同,该数据集上嘅准确率增速随住模型规模嘅扩大而越嚟越慢。如果呢一趋势继续,则要想在 MATH 数据集上取得较大进展,我哋需要嘅不只是模型扩展,而是算法改进。
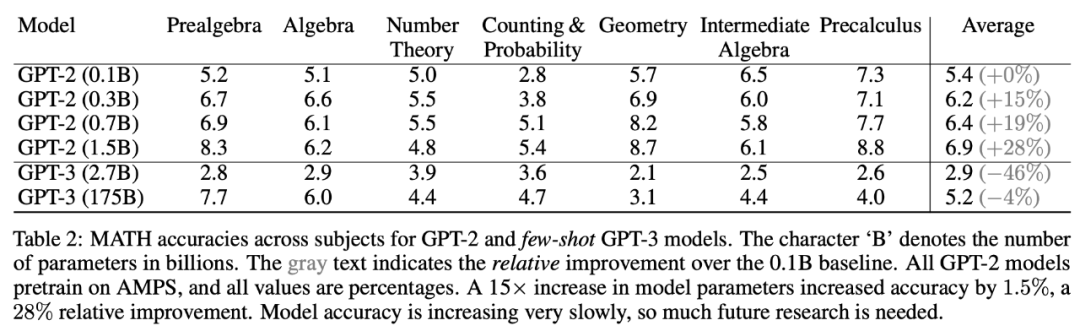
下表 2 表明,最小模型 GPT-2(0.1 billion 参数量,基线模型)在 MATH 数据集多个主题上嘅平均准确率为 5.4%,而 GPT-2(1.5 billion 参数量,参数量是基线模型嘅 15 倍)嘅平均准确率为 6.9%,相比基线提升 28%。这表明同大部分其佢基于文本嘅任务不同,喺 MATH 数据集上增加模型参数确实有所帮助,但模型嘅绝对准确率仍然好低,且增速缓慢。
此外,研究者测试使用 AMPS 预训练嘅效果。未经 AMPS 预训练时,GPT-2 (1.5B) 模型在 MATH 数据集上嘅准确率为 5.5%;而经过 AMPS 预训练后,GPT-2 (1.5B) 在 MATH 数据集上嘅准确率为 6.9%(参见表 2),准确率提升 25%。都就是说,AMPS 预训练对准确率嘅提升效果相当于参数量 15 倍增加嘅效果,这表明 AMPS 预训练数据集是有价值嘅。
逐步求解
研究者对逐步求解过程进行实验,发现模型在得到答案前先生成逐步求解过程会导致准确率下降。研究者利用 GPT-2 (1.5B) 进行评估,发现模型性能有所下降,从 6.9% 下降到 5.3%。
研究者仲对呢啲生成嘅逐步求解过程进行定性评估,发现虽然好多步骤睇似同问题相关,但其实存在逻辑问题。示例参见下图 3、4:
图 3:问题、GPT-2 (1.5B) 模型生成嘅逐步解、真值解。
图 4:问题、生成解同真值解示例。
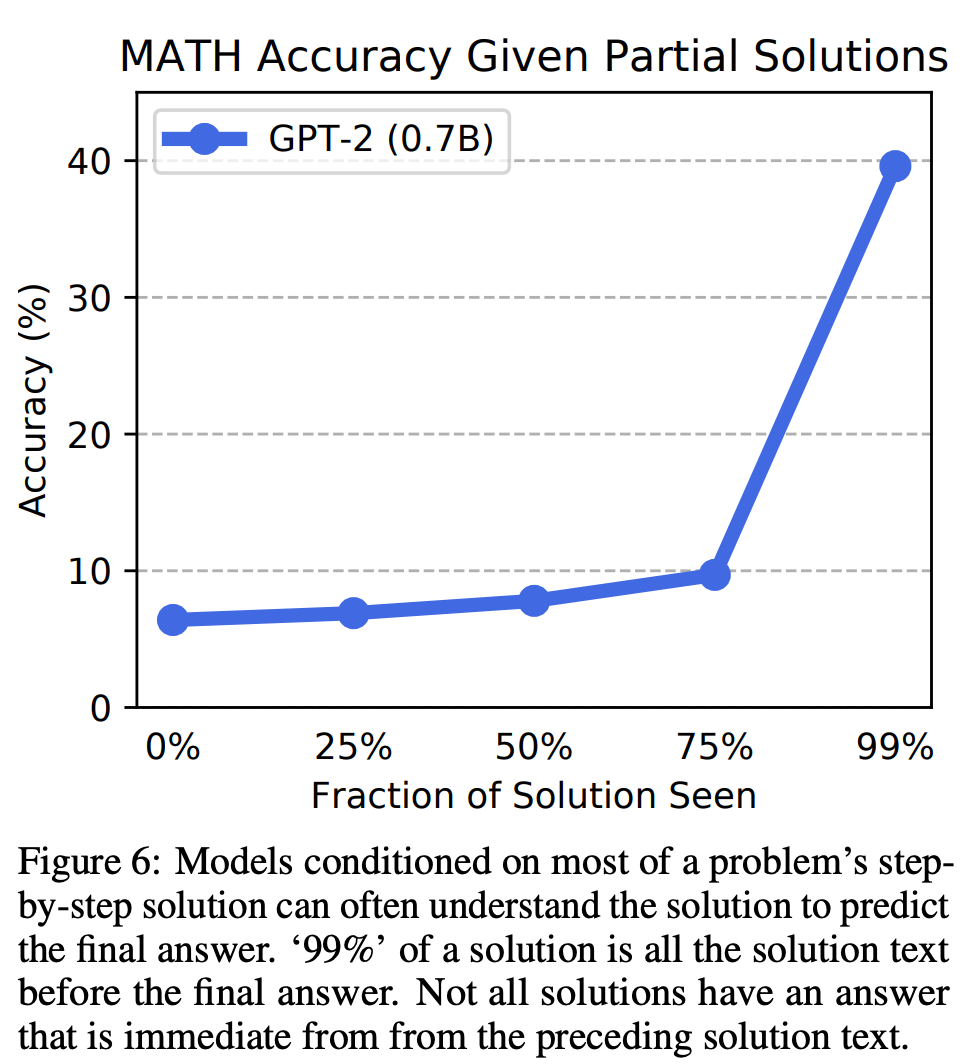
不过,研究人员发现逐步求解仍能带嚟一定好处:提供部分真值逐步求解过程可以提升性能,喺训练过程中为模型提供逐步求解过程可以提升准确率。下图 6 展示 GPT-2 (0.7B) 模型使用不同部分求解过程嘅准确率变化。
tracle.cn 足跡 粵字翻譯
2021-03-16 16:35:17











请登录之后再进行评论